Sinusoïdal
Square
Triangular
Pulse
1- ANALYSIS OF BASIC SIGNALS : SINE, SQUARE , TRIANGULAR AND PULSE WAVES.
1- The theory of signal analysis : We represent a signal in two different domains :
- Time domain : It is simply an algebraic expression written as v(t). In practice we use an oscilloscope to view the signal in the time domain.
- Frequency domain : The mathematical representation is more complex, we use Fourier analysis for periodic signals to find their frequency components. Fourier analysis stipulates that all periodic signals
can be replaced by a sum of sines and cosines functions with different amplitudes as it is shown by the following equation :

With a0, aN and bN called the Fourier series coefficient and they can be found by using the following equations :



Our objective is to use the results of the calculations of the coefficients and apply it in the spectral analysis of periodic signals.In practice we use a spectrum analyser
to view the signal in the frequency domain where the horizontal axis will represent the frequency f and the vertical one the voltage in Volts or the power in dBm as it is the case in telecommunications.
1.1- Sinusoïdal Waveform : This is the simplest form of a signal. In the frequency domain it is represented by an impulse situated at the value of the frequency f of the signal along the f-axis. The
same result applies to a cosine or any sine waveform with a phase angle.
1.2- Square Wave : Fourier analysis and coefficients calculations show us that a square waveform is an infinite sum of sines. The frequency of every sine is an odd multiple of the square waveform frequency
called the fundamental frequency while it's odd multiples are called the harmonics. For example a square wave at a frequency of 100 kHz can be represented by the summation of an infinite number of sine waves
at 100, 300, 500 kHz .. . The amplitude of every sine is given by the following relation :

1.3- Triangular Waveform : Like the square waveform, the triangular waveform is also a sum of an infinite number of sine waves with the frequency of each sine an odd multiple of the fundamental's. However the
amplitude of the sines is a lot smaller and given by the following equation :
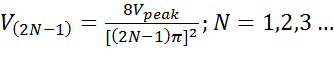
1.4-Pulse Train : The parameters of the pulse waveform are shown in the figure below :
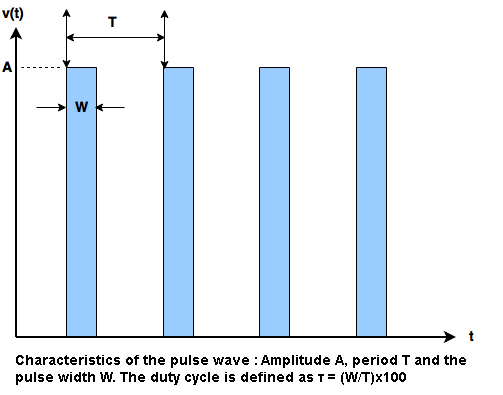
The fourier coefficients of the wave are given by the following expressions :



Note that the order of the harmonics can be both even and odd depending on the value of the duty cycle of the wave.

With a0, aN and bN called the Fourier series coefficient and they can be found by using the following equations :



Our objective is to use the results of the calculations of the coefficients and apply it in the spectral analysis of periodic signals.In practice we use a spectrum analyser to view the signal in the frequency domain where the horizontal axis will represent the frequency f and the vertical one the voltage in Volts or the power in dBm as it is the case in telecommunications.